Тред №324431

Но давайте дальше разберемся, что же означает уравнение (21.39), что именно у нас будет сплюснуто в  γ  раз. А сплюснутыми оказываются эквипотенциальные поверхности, которые «заморожены» относительно источника:
 

 
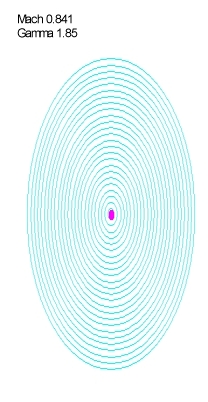
В то же время, сферические фронты волн  φ  по-прежнему распространяются со скоростью света во все стороны от тех точек, где находился источник в момент их излучения:
 

 
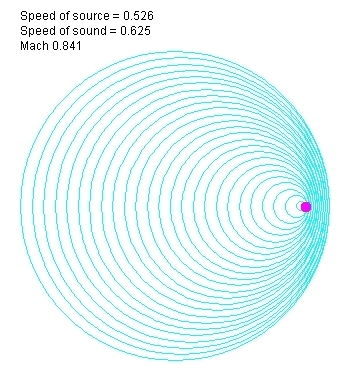
Подчеркну, что так выглядит картина распространения фронтов волн и эквипотенциальные поверхности в обеих системах отсчета (точнее, во всех инерциальных СО). В СО покоящейся среды, фронты волн распространяются по формуле:

(x – ξ)² + y² + z² = c²(t – ԏ)²

или, для  i-ой единичной волны:

(x – v i dt)² + y² + z² = c² (t – i dt)²

При переходе в СО источника, воспользуемся преобразованием Галилея   x = u + vt.  Получим

(u + vt – vԏ)² + y² + z² = c²(t – ԏ)²

или

(u + v (t – i dt))² + y² + z² = c² (t – i dt)²

Это уравнение описывает сферические фронты волн, распространяющиеся со скоростью  c  и «сдуваемые» встречным ветром со скоростью  –v.  Галилей по-прежнему рулит, хотя теперь эквипотенциальные поверхности больше не выглядят так же, как фронты волн (см. предыдущий раздел).

Как я уже говорил, вывод уравнения Лиенара-Вихерта не содержит в себе ничего специфического только для уравнений Максвелла, для скорости света. Если уравнение для запаздывающего потенциала  φ  действительно корректно, то оно должно относиться ко всем другим волнам. В частности, тогда уравнение для звукового давления тоже должно включать в себя ЛВД множитель:

p = pₐa / (r’ – r’∙v / c)) = pₐa / (r’ (1 – β cos α)). 

При одном и том же значении  r'  (т.е. на поверхности сферы радиусом  r' ),  значения  p  будут отличаться – они будут максимальны спереди от движущегося источника и минимальны сзади от него. Давайте посмотрим, что произойдет, если мы будем постепенно уменьшать радиус  r'.  Очевидно, величина  p  будет возрастать обратно пропорционально уменьшению  r',  тогда как относительные значения  p  в разных местах сферы меньшего радиуса останутся такими же, как у сферы большего радиуса (в сферических координатах, зависимость  p  от  углов  θ  и  φ  одинакова при любом  r' ).  Все более уменьшая  r',  в пределе мы дойдем до поверхности источника – сферы радиуса  a.  Прямо над этой поверхностью, давление  pₐ  тоже должно подчиняться зависимости

pₐ= pₐ₀ / (1 – β cos α)

где  pₐ₀ – давление на поверхности источника (радиуса  a),  когда источник покоится относительно среды; оно одинаково во всех точках этой поверхности.

То есть  pₐ(a, α) более не одинакова во всех точках поверхности источника, как мы постулировали вначале.

Но это означает, что в вышеприведенное уравнение для давления должно входить не  pₐ,  а  pₐ₀:

p = pₐ₀a / (r’ – r’∙v / c)) = pₐ₀a / (r’ (1 – β cos α))

что эквивалентно

p = pₐ(a, α) a / r’

Давайте разберемся, что это означает. Во-первых, это означает, что при движении источника в разных точках его поверхности давление различается. Спереди от источника (угол  α  меньше 90°), давление становится больше в  1 / (1 – β cos α)  раз, а сзади (угол  α  больше 90°) – меньше. Вообще говоря, эта идея кажется достаточно логичной: благодаря движению источника, спереди от него жидкость, действительно, может стать плотнее, а сзади – более разреженной, по сравнению с покоящимся источником. Во-вторых, это означает, что давление на расстоянии от источника определяется именно распределением давления на поверхности источника, оно передается во все стороны без искажений (в «нулевом приближении»). А это означает, что уравнение Лиенара-Вихерта неверно.

Как это? А вот так – при выводе этого уравнения утверждается, что ЛВД множитель возникает именно из-за запаздывания, из-за того, что интеграл как-то там проносится над зарядом и т.д. Если же этот множитель возникает из-за того, что давление в разных точках поверхности источника неодинаково и имеет следующую зависимость

pₐ= pₐ₀ / (1 – β cos α)

то запаздывание и процедура интегрирования в движении здесь совершенно ни при чем. Собственно говоря, если  зависимость  pₐ от, допустим, углов  θ  и  φ, в сферических координатах, имеет другой характер, то и давление на расстоянии от источника будет иметь точно такой же характер. Потому что совсем не обязательно, чтобы  pₐ  имела непременно такую зависимость:

pₐ= pₐ₀ / (1 – β cos α)

Зависимость эту надо определять отдельно, из других физических соображений. Даже если,  допустим, для сферы зависимость именно такая, то для источника с другой формой поверхности она будет подчиняться какому-то другому уравнению.

Аналогично, для движущегося сферического заряда радиуса  a  мы получим, что потенциал  φ  у самой его поверхности подчиняется уравнению

φₐ= φₐ₀ / (1 – β cos α)

где  φₐ₀ – потенциал рядом с поверхностью заряда (на бесконечно малом расстоянии от нее), когда заряд покоится относительно среды.

Это, по-видимому, означает, что при движении заряда его поверхностная плотность не одинакова в разных точках или объемная плотность неодинакова во всем объеме заряда. Теоретически, это можно проверить, если исследовать движение заряженной сферы в вакууме и перераспределение зарядов на ее поверхности. Причем измерять надо не напряженность электрического поля вокруг заряда (потому что одни и те же изменения поля можно интерпретировать по-разному, как в рамках «классической» теории, так и в рамках моей теории), а само распределение зарядов (или токи) на поверхности сферы. Но при тех скоростях, которые достижимы в настоящее время, зарегистрировать такое перераспределение зарядов будет не так просто.