Жизнь, Разум, Человек, Религия и Наука
145,946
565
|
|
Yuri Rus ( Слушатель ) |
| 24 май 2011 08:08:21 |
Тред №324430
новая дискуссия Дискуссия 526
Давайте посмотрим, как Фейнман выводит первое преобразование Лоренца, также известное как сокращение длины Фитцджеральда-Лоренца.
Фейнман Р., Лейтон Р., Сэндс М. «Фейнмановские Лекции по Физике», т. 6 «Электродинамика», гл. 21, § 5-6, стр. 156-163:


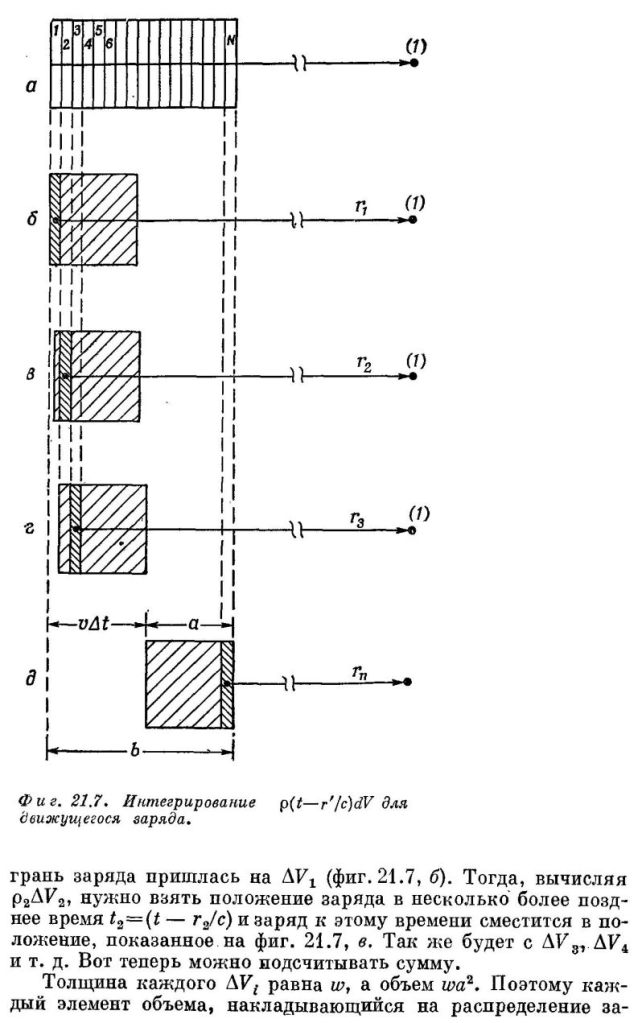





Здесь в формуле (21.39) опечатка – отсутствует знак корня у второго выражения (1 – β²). Вот эта формула из английского издания:
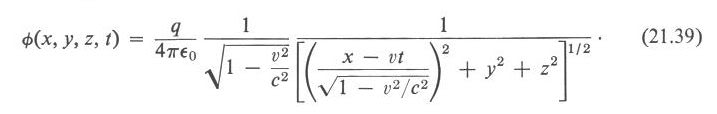
Пойдем по порядку. Уравнения (21.33) и (21.34), запаздывающие потенциалы Лиенара-Вихерта, по сравнению с используемым мной выше уравнением для звукового давления, содержат дополнительный множитель, такой же, как в эффекте Доплера (назовем его ЛВД множителем, Лиенара-Вихерта-Доплера):
1 / (1 – r’∙v / (r’c)) ≡ 1 / (1 – β cos α)
Именно благодаря наличию ЛВД множителя у потенциала φ, вместо уравнения
φ(x, y, z, t) = q (1 – β²) / (4πε₀ (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½))
возникает уравнение (21.39).
Таким образом, уравнения Лиенара-Вихерта, можно сказать, ответственны за возникновение преобразований Лоренца и теории относительности (хотя, как я уже писал, они вытекают и из определения полного дифференциала, и вообще из самого мат. аппарата физики). Я пока не хочу анализировать вывод этих уравнений для запаздывающих потенциалов; я это сделаю несколько позже. Сейчас же, временно, примем, что эти уравнения правильные, ЛВД множитель должен присутствовать в уравнениях для потенциалов. Сразу же можно сказать, что тогда этот множитель должен присутствовать и в уравнении для звукового давления, генерируемого движущимся источником. В выводе уравнений Лиенара-Вихерта нет ничего, что привязывало бы их только к уравнениям Максвелла и к абсолютному пределу – скорости света. Особенно это очевидно, когда вывод делается при помощи функций Грина и дельта-функции Дирака.
Стоит отметить следующее. В предыдущем разделе, когда я выводил формулы для звукового давления и силы давления, я сначала получил формулы для фиксированных значениях координат и времени: для одной единичной волны, излученной в начальный момент времени из начала координат, которая оказалась в определенной точке в фиксированный момент времени. Потом я перешел в СО источника и пересчитал давление и силу для этой точки в координатах источника. Только потом я распространил эти результаты на переменные координаты и время, и из СО источника вернулся в СО покоящейся среды. Из этого анализа было очевидно, что в обеих системах отсчета уравнения выглядят одинаково, а переход между ними осуществляется при помощи преобразования Галилея. Два наблюдателя, один в СО покоящейся среды и другой в СО источника, будут видеть распространение волн абсолютно одинаково.
Фейнман же использовал другой, более короткий вывод уравнения для потенциала, оставаясь все время только в СО покоящейся среды. В самом конце он, глядя на полученную формулу, делает предположение, что в СО источника это уравнение должно выглядеть совершенно иначе – а именно, так, как выглядело бы уравнение покоящегося источника в покоящейся среде. Я говорю «Фейнман» – подразумеваю всех физиков. Не он первым получил это уравнение и в книге дана не его личная, а общепринятая в современной физике интерпретация этого уравнения (в конце XIX века, оно интерпретировалось с позиции теории эфира).
Если же мы повторим ту же стратегию вывода уравнений для φ в системах отсчета покоящейся среды и источника, как в предыдущем разделе было сделано для звукового давления, мы увидим, что в обеих системах отсчета эти уравнения выглядят одинаково, что переход между этими СО осуществляется при помощи преобразования Галилея и что наблюдатель в СО источника будет регистрировать «сдувание встречным ветром» излучаемых источником волн.
Итак, проделаем весь анализ заново. Вначале я буду следовать Фейнману и покажу, что означает его вывод для фиксированных значений (их фиксированность подчеркнута нижним индексом 1 или 2).
Обратим внимание, что в главе 6 у Фейнмана выбор нулевого момента времени произволен, так же как и выбор начала координат. Мы можем выбрать их любым удобным для нас способом – и самым удобным в данной ситуации является такой вариант, при котором t' = 0 и в этот нулевой момент времени заряд находится в начале координат. То есть отсчет времени логично начинать в тот момент, когда заряд излучает сферическую волну потенциала φ₁, которая в момент времени t₁ достигает точки P(x₁, y₁, z₁), тогда как заряд в момент t₁ оказывается в точке с координатами (vt₁, 0, 0). Это позволяет нам значительно упростить все рассуждения, нисколько не меняя их смысла, и формулы Фейнмана будут переписаны так:
t₁ = r₁’/c (21.35)’
r₁’ = (x₁² + y₁² + z₁²)½ (21.36)’
Следующие 2 уравнения, при t’ = 0, сводятся к
c²t₁² = x₁² + y₁² + z₁²
К этому же выражению сводится и уравнение
t₁ – vx₁/c² = ((x₁ – vt₁)² + (1 – β²) (y₁² + z₁²))½) / c (21.37)’
которое, после возведения левой и правой частей в квадрат, станет
c²t₁² (1 – β²) = x₁² (1 – β²) + (y₁² + z₁²) (1 – β²)
то есть опять же превратится в
c²t₁² = x₁² + y₁² + z₁²
Далее, r₁' = ct₁, а уравнение для потенциала φ₁ станет
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (r₁’ – r₁’∙v / c)) (21.38 )’
Составляющая v в направлении r₁' равна vx₁/r₁', так что v∙r₁' просто равно vx₁, а весь знаменатель равен
ct₁ – vx₁/c = c (t₁ – vx₁/c²)
Подставив это в уравнение (21.38 ), получим
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (ct₁ – vx₁/c)) (21.39)’
То есть это всё то же уравнение для потенциала Лиенара-Вихерта (для фиксированной точки, фиксированного момента времени и одной единичной волны, излученной в нулевой момент времени), а не
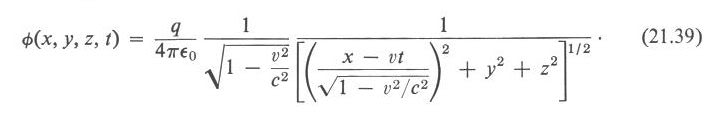
Теперь, чтобы получить уравнения для φ в системах отсчета покоящейся среды и источника при переменных координатах и времени, воспользуемся той же стратегией, как в предыдущем разделе было сделано для звукового давления.
Пусть в момент времени t = 0 заряд излучает первую сферическую единичную волну потенциала φ, которая распространяется по закону
r₁(t) = ct = i x(t) + j y(t) + k z(t)
или
x²(t) + y²(t) + z²(t) = c²t²
Будем полагать, что потенциал φ₁ в каждой точке этой единичной волны меняется по формуле Лиенара-Вихерта:
φ₁(x, y, z, t) = q / (4πε₀ ((x² + y² + z²)½ – vx/c)) = q / (4πε₀ (ct – vx/c))
В момент времени t₁, первая волна достигает точки P₁(x₁, y₁, z₁). Потенциал φ₁ в этой точке равен
φ₁(x₁, y₁, z₁, t₁) = q / (4πε₀ ((x₁² + y₁² + z₁²)½ – vx₁/c)) = q / (4πε₀ (ct₁ – vx₁/c))
Из-за ЛВД множителя, эквипотенциальные поверхности больше не совпадают с фронтами волн φ, поэтому вектор ∇φ более не параллелен вектору r’. Мы, конечно, можем определить направление градиента по частям, определив значения ∂φ/∂x, ∂φ/∂y, ∂φ/∂z, а потом еще добавить ∂Ax/∂t, ∂Ay/∂t, ∂Az/∂t. Именно так делал Фейнман в главе 26. Но мы пока этого делать не будем, это только даст много непринципиальной писанины. Возможно, потом.
Сейчас определим только, чему равна производная φ по r’ в точке (x₁, y₁, z₁) в момент t₁, т.е. Δφ₁ / Δr₁’. Это будет нам более полезно.
За время dt, источник сместился из начала координат в точку (v dt, 0, 0). В момент времени dt, источник излучает вторую сферическую единичную волну φ, которая распространяется по закону
r₂(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
Потенциал φ₂ в каждой точке второй единичной волны будет меняться по закону:
φ₂(x, y, z, t) = q / (4πε₀ (((x – v dt)² + y² + z²)½ – v(x – v dt)/c)) = q / (4πε₀ (c(t – dt) – v(x – v dt)/c))
Вторая единичная волна за время t₁ – dt проходит расстояние c (t₁ – dt) во все стороны. В направлении r₁’, эта волна в момент времени t₁ окажется в точке P₂(x₂, y₂, z₂), на расстоянии Δr₁’ от точки P₁. Это расстояние, очевидно, равно расстоянию c dt, которое не прошла вторая единичная волна по сравнению с первой, минус проекцию расстояния v dt на направление r₁', то есть c dt β cos α₁:
Δr₁’ = c dt (1 – r₁’∙v / (r₁’c)) ≡ c dt (1 – β cos α₁).
Потенциал φ₂ в этой точке равен
φ₂( x₂, y₂, z₂, t₁) = q / (4πε₀c (t₁ – dt) (1 – β cos α₁))
Итак, производная φ по r’ в точке (x₁, y₁, z₁) в момент t₁ будет равна:
Δφ₁ / Δr₁’ = (φ₁(t₁) – φ₂(t₁)) / (c dt (1 – β cos α₁)) =
= – q / (4πε₀ (r₁’² (1 – β cos α₁)²)) = – q / (4πε₀ ((c t₁)² (1 – β cos α₁)²))
Мы видим, что Δφ₁ / Δr₁’ отличается от φ₁ появлением второго ЛВД множителя, то есть 1 / (1 – β cos α₁). В предыдущем разделе, когда мы предположили, что фронты волн и эквипотенциальные поверхности совпадают, Δp₁ / Δr₁’ отличалась от p₁ точно таким же ЛВД множителем. Этот же множитель появляется и для частоты звуковой волны, если источник движется. Везде – по той же самой причине. Для простоты, примем, что наблюдатель (детектор) находится на оси х. Спереди от источника, фронты волн будут расположены в 1/(1 – β) раз чаще, а сзади – в 1/(1 + β) раз реже, чем у покоящегося источника. Но эти фронты волн соответствуют разным значениям φ или p. Чем чаще расположены фронты последовательных волн, тем круче падение кривой φ или p, тем больше значение соответствующей производной.
Любая переменная f, для которой можно записать волновое уравнение вида
∂²f/∂t² – c²∇²f = S(x – ξ, y, z, t – ԏ)
имеет фронты волн, распространяющиеся со скоростью c. Производная f по r’ всегда будет приобретать ЛВД множитель, каков бы ни был вид зависимости самой f от r’.
Теперь перейдем в СО источника, используя преобразование Галилея для координат:
r₁ = ((x₁ – vt₁)² + y₁² + z₁²)½
u₁ = x₁ – vt₁ = x₁ – βr₁’
и перепишем уравнение для φ₁ в точке P₁ относительно координат источника в момент t₁, а не относительно запаздывающих, координат источника в нулевой момент времени.
Полностью аналогично тому, как это было сделано выше для звукового давления, из уравнения
r₁'² = x₁² + y₁² + z₁² = (u₁ + βr₁’)² + y₁² + z₁²
раскрыв скобки в (u₁ + βr₁’)² и перенеся все налево, путем решения квадратного уравнения относительно степеней r₁', мы получим:
r₁' = (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½) / (1 – β²)
r₁’ (1 – β cos α₁) = (1 – β²) r₁’ – β u₁ = (u₁² + (1 – β²) (y₁² + z₁²))½
Тогда φ₁ в СО источника равен:
φ₁(u₁, y₁, z₁) = q / (4πε₀ (u₁² + (1 – β²) (y₁² + z₁²))½)
Остановимся на секунду. До сих пор все эти рассуждения и уравнения относились только к фиксированным значениям (одна единичная волна, излученная в нулевой момент времени и в другой момент достигающая определенной точки). Обратите внимание – только когда мы перешли в СО источника, воспользовавшись для этого преобразованием Галилея, а не Лоренца, мы получили уравнение, аналогичное уравнению (21.39) Фейнмана.
Тогда как раньше, напомню, для этих же фиксированных значений в СО покоящейся среды мы имели всего лишь уравнение для потенциала Лиенара-Вихерта:
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (ct₁ – vx₁/c)) (21.39)’
Теперь перейдем от фиксированных значений x₁, y₁, z₁, u₁, t₁ к переменным x, y, z, u, t. Введем их при помощи переменного коэффициента ω:
u = ω u₁ y = ω y₁ z = ω z₁ r = ω r₁
Тогда φ в произвольной точке P(u, y, z) будет равен:
φ(u, y, z) = q / (4πε₀ (u² + (1 – β²) (y² + z²))½)
Теперь давайте совершим обратный переход в СО покоящейся среды. Заменим
u = x – vt
где vt – это положение источника в момент t.
φ(x, y, z, t) = q / (4πε₀ ((x – vt)² + (1 – β²) (y² + z²))½) ≡
≡ q / (4πε₀ (1 – β²)½ ((x – vt)² / (1 – β²) + y² + z²)½)
Это уравнение полностью совпадает с уравнением Фейнмана (21.39). Здесь Фейнман написал:

Однако, как мы видели, это не так: для вывода этих уравнений, мы из СО покоящейся среды перешли в СО источника, причем именно при помощи преобразования Галилея u = x – vt, затем обратно. И в обеих этих системах отсчета, уравнения для φ выглядят совершенно одинаково (единственная разница – замена u на x – vt). Потенциал φ в СО источника выглядит как
φ(u, y, z) = q / (4πε₀ (u² + (1 – β²) (y² + z²))½)
а вовсе не как
φ(u, y, z) = q / (4πε₀ (u² + y² + z²)½)
Это я и имел в виду, когда писал, что Фейнман дает формуле (21.39) совершенно неправильную интерпретацию, в частности, потому, что у него отсутствует переход из одной системы отсчета в другую при выводе этих уравнений.
Фейнман Р., Лейтон Р., Сэндс М. «Фейнмановские Лекции по Физике», т. 6 «Электродинамика», гл. 21, § 5-6, стр. 156-163:








Здесь в формуле (21.39) опечатка – отсутствует знак корня у второго выражения (1 – β²). Вот эта формула из английского издания:
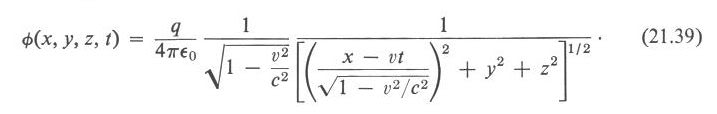
Пойдем по порядку. Уравнения (21.33) и (21.34), запаздывающие потенциалы Лиенара-Вихерта, по сравнению с используемым мной выше уравнением для звукового давления, содержат дополнительный множитель, такой же, как в эффекте Доплера (назовем его ЛВД множителем, Лиенара-Вихерта-Доплера):
1 / (1 – r’∙v / (r’c)) ≡ 1 / (1 – β cos α)
Именно благодаря наличию ЛВД множителя у потенциала φ, вместо уравнения
φ(x, y, z, t) = q (1 – β²) / (4πε₀ (β (x – vt) + ((x – vt)² + (1 – β²) (y² + z²))½))
возникает уравнение (21.39).
Таким образом, уравнения Лиенара-Вихерта, можно сказать, ответственны за возникновение преобразований Лоренца и теории относительности (хотя, как я уже писал, они вытекают и из определения полного дифференциала, и вообще из самого мат. аппарата физики). Я пока не хочу анализировать вывод этих уравнений для запаздывающих потенциалов; я это сделаю несколько позже. Сейчас же, временно, примем, что эти уравнения правильные, ЛВД множитель должен присутствовать в уравнениях для потенциалов. Сразу же можно сказать, что тогда этот множитель должен присутствовать и в уравнении для звукового давления, генерируемого движущимся источником. В выводе уравнений Лиенара-Вихерта нет ничего, что привязывало бы их только к уравнениям Максвелла и к абсолютному пределу – скорости света. Особенно это очевидно, когда вывод делается при помощи функций Грина и дельта-функции Дирака.
Стоит отметить следующее. В предыдущем разделе, когда я выводил формулы для звукового давления и силы давления, я сначала получил формулы для фиксированных значениях координат и времени: для одной единичной волны, излученной в начальный момент времени из начала координат, которая оказалась в определенной точке в фиксированный момент времени. Потом я перешел в СО источника и пересчитал давление и силу для этой точки в координатах источника. Только потом я распространил эти результаты на переменные координаты и время, и из СО источника вернулся в СО покоящейся среды. Из этого анализа было очевидно, что в обеих системах отсчета уравнения выглядят одинаково, а переход между ними осуществляется при помощи преобразования Галилея. Два наблюдателя, один в СО покоящейся среды и другой в СО источника, будут видеть распространение волн абсолютно одинаково.
Фейнман же использовал другой, более короткий вывод уравнения для потенциала, оставаясь все время только в СО покоящейся среды. В самом конце он, глядя на полученную формулу, делает предположение, что в СО источника это уравнение должно выглядеть совершенно иначе – а именно, так, как выглядело бы уравнение покоящегося источника в покоящейся среде. Я говорю «Фейнман» – подразумеваю всех физиков. Не он первым получил это уравнение и в книге дана не его личная, а общепринятая в современной физике интерпретация этого уравнения (в конце XIX века, оно интерпретировалось с позиции теории эфира).
Если же мы повторим ту же стратегию вывода уравнений для φ в системах отсчета покоящейся среды и источника, как в предыдущем разделе было сделано для звукового давления, мы увидим, что в обеих системах отсчета эти уравнения выглядят одинаково, что переход между этими СО осуществляется при помощи преобразования Галилея и что наблюдатель в СО источника будет регистрировать «сдувание встречным ветром» излучаемых источником волн.
Итак, проделаем весь анализ заново. Вначале я буду следовать Фейнману и покажу, что означает его вывод для фиксированных значений (их фиксированность подчеркнута нижним индексом 1 или 2).
Обратим внимание, что в главе 6 у Фейнмана выбор нулевого момента времени произволен, так же как и выбор начала координат. Мы можем выбрать их любым удобным для нас способом – и самым удобным в данной ситуации является такой вариант, при котором t' = 0 и в этот нулевой момент времени заряд находится в начале координат. То есть отсчет времени логично начинать в тот момент, когда заряд излучает сферическую волну потенциала φ₁, которая в момент времени t₁ достигает точки P(x₁, y₁, z₁), тогда как заряд в момент t₁ оказывается в точке с координатами (vt₁, 0, 0). Это позволяет нам значительно упростить все рассуждения, нисколько не меняя их смысла, и формулы Фейнмана будут переписаны так:
t₁ = r₁’/c (21.35)’
r₁’ = (x₁² + y₁² + z₁²)½ (21.36)’
Следующие 2 уравнения, при t’ = 0, сводятся к
c²t₁² = x₁² + y₁² + z₁²
К этому же выражению сводится и уравнение
t₁ – vx₁/c² = ((x₁ – vt₁)² + (1 – β²) (y₁² + z₁²))½) / c (21.37)’
которое, после возведения левой и правой частей в квадрат, станет
c²t₁² (1 – β²) = x₁² (1 – β²) + (y₁² + z₁²) (1 – β²)
то есть опять же превратится в
c²t₁² = x₁² + y₁² + z₁²
Далее, r₁' = ct₁, а уравнение для потенциала φ₁ станет
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (r₁’ – r₁’∙v / c)) (21.38 )’
Составляющая v в направлении r₁' равна vx₁/r₁', так что v∙r₁' просто равно vx₁, а весь знаменатель равен
ct₁ – vx₁/c = c (t₁ – vx₁/c²)
Подставив это в уравнение (21.38 ), получим
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (ct₁ – vx₁/c)) (21.39)’
То есть это всё то же уравнение для потенциала Лиенара-Вихерта (для фиксированной точки, фиксированного момента времени и одной единичной волны, излученной в нулевой момент времени), а не
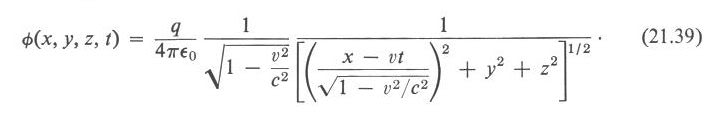
Теперь, чтобы получить уравнения для φ в системах отсчета покоящейся среды и источника при переменных координатах и времени, воспользуемся той же стратегией, как в предыдущем разделе было сделано для звукового давления.
Пусть в момент времени t = 0 заряд излучает первую сферическую единичную волну потенциала φ, которая распространяется по закону
r₁(t) = ct = i x(t) + j y(t) + k z(t)
или
x²(t) + y²(t) + z²(t) = c²t²
Будем полагать, что потенциал φ₁ в каждой точке этой единичной волны меняется по формуле Лиенара-Вихерта:
φ₁(x, y, z, t) = q / (4πε₀ ((x² + y² + z²)½ – vx/c)) = q / (4πε₀ (ct – vx/c))
В момент времени t₁, первая волна достигает точки P₁(x₁, y₁, z₁). Потенциал φ₁ в этой точке равен
φ₁(x₁, y₁, z₁, t₁) = q / (4πε₀ ((x₁² + y₁² + z₁²)½ – vx₁/c)) = q / (4πε₀ (ct₁ – vx₁/c))
Из-за ЛВД множителя, эквипотенциальные поверхности больше не совпадают с фронтами волн φ, поэтому вектор ∇φ более не параллелен вектору r’. Мы, конечно, можем определить направление градиента по частям, определив значения ∂φ/∂x, ∂φ/∂y, ∂φ/∂z, а потом еще добавить ∂Ax/∂t, ∂Ay/∂t, ∂Az/∂t. Именно так делал Фейнман в главе 26. Но мы пока этого делать не будем, это только даст много непринципиальной писанины. Возможно, потом.
Сейчас определим только, чему равна производная φ по r’ в точке (x₁, y₁, z₁) в момент t₁, т.е. Δφ₁ / Δr₁’. Это будет нам более полезно.
За время dt, источник сместился из начала координат в точку (v dt, 0, 0). В момент времени dt, источник излучает вторую сферическую единичную волну φ, которая распространяется по закону
r₂(t) – v dt = c (t – dt)
или
(x(t) – v dt)² + y²(t) + z²(t) = c² (t – dt)²
Потенциал φ₂ в каждой точке второй единичной волны будет меняться по закону:
φ₂(x, y, z, t) = q / (4πε₀ (((x – v dt)² + y² + z²)½ – v(x – v dt)/c)) = q / (4πε₀ (c(t – dt) – v(x – v dt)/c))
Вторая единичная волна за время t₁ – dt проходит расстояние c (t₁ – dt) во все стороны. В направлении r₁’, эта волна в момент времени t₁ окажется в точке P₂(x₂, y₂, z₂), на расстоянии Δr₁’ от точки P₁. Это расстояние, очевидно, равно расстоянию c dt, которое не прошла вторая единичная волна по сравнению с первой, минус проекцию расстояния v dt на направление r₁', то есть c dt β cos α₁:
Δr₁’ = c dt (1 – r₁’∙v / (r₁’c)) ≡ c dt (1 – β cos α₁).
Потенциал φ₂ в этой точке равен
φ₂( x₂, y₂, z₂, t₁) = q / (4πε₀c (t₁ – dt) (1 – β cos α₁))
Итак, производная φ по r’ в точке (x₁, y₁, z₁) в момент t₁ будет равна:
Δφ₁ / Δr₁’ = (φ₁(t₁) – φ₂(t₁)) / (c dt (1 – β cos α₁)) =
= – q / (4πε₀ (r₁’² (1 – β cos α₁)²)) = – q / (4πε₀ ((c t₁)² (1 – β cos α₁)²))
Мы видим, что Δφ₁ / Δr₁’ отличается от φ₁ появлением второго ЛВД множителя, то есть 1 / (1 – β cos α₁). В предыдущем разделе, когда мы предположили, что фронты волн и эквипотенциальные поверхности совпадают, Δp₁ / Δr₁’ отличалась от p₁ точно таким же ЛВД множителем. Этот же множитель появляется и для частоты звуковой волны, если источник движется. Везде – по той же самой причине. Для простоты, примем, что наблюдатель (детектор) находится на оси х. Спереди от источника, фронты волн будут расположены в 1/(1 – β) раз чаще, а сзади – в 1/(1 + β) раз реже, чем у покоящегося источника. Но эти фронты волн соответствуют разным значениям φ или p. Чем чаще расположены фронты последовательных волн, тем круче падение кривой φ или p, тем больше значение соответствующей производной.
Любая переменная f, для которой можно записать волновое уравнение вида
∂²f/∂t² – c²∇²f = S(x – ξ, y, z, t – ԏ)
имеет фронты волн, распространяющиеся со скоростью c. Производная f по r’ всегда будет приобретать ЛВД множитель, каков бы ни был вид зависимости самой f от r’.
Теперь перейдем в СО источника, используя преобразование Галилея для координат:
r₁ = ((x₁ – vt₁)² + y₁² + z₁²)½
u₁ = x₁ – vt₁ = x₁ – βr₁’
и перепишем уравнение для φ₁ в точке P₁ относительно координат источника в момент t₁, а не относительно запаздывающих, координат источника в нулевой момент времени.
Полностью аналогично тому, как это было сделано выше для звукового давления, из уравнения
r₁'² = x₁² + y₁² + z₁² = (u₁ + βr₁’)² + y₁² + z₁²
раскрыв скобки в (u₁ + βr₁’)² и перенеся все налево, путем решения квадратного уравнения относительно степеней r₁', мы получим:
r₁' = (β u₁ + (u₁² + (1 – β²) (y₁² + z₁²))½) / (1 – β²)
r₁’ (1 – β cos α₁) = (1 – β²) r₁’ – β u₁ = (u₁² + (1 – β²) (y₁² + z₁²))½
Тогда φ₁ в СО источника равен:
φ₁(u₁, y₁, z₁) = q / (4πε₀ (u₁² + (1 – β²) (y₁² + z₁²))½)
Остановимся на секунду. До сих пор все эти рассуждения и уравнения относились только к фиксированным значениям (одна единичная волна, излученная в нулевой момент времени и в другой момент достигающая определенной точки). Обратите внимание – только когда мы перешли в СО источника, воспользовавшись для этого преобразованием Галилея, а не Лоренца, мы получили уравнение, аналогичное уравнению (21.39) Фейнмана.
Тогда как раньше, напомню, для этих же фиксированных значений в СО покоящейся среды мы имели всего лишь уравнение для потенциала Лиенара-Вихерта:
φ₁ (x₁, y₁, z₁, t₁) = q / (4πε₀ (ct₁ – vx₁/c)) (21.39)’
Теперь перейдем от фиксированных значений x₁, y₁, z₁, u₁, t₁ к переменным x, y, z, u, t. Введем их при помощи переменного коэффициента ω:
u = ω u₁ y = ω y₁ z = ω z₁ r = ω r₁
Тогда φ в произвольной точке P(u, y, z) будет равен:
φ(u, y, z) = q / (4πε₀ (u² + (1 – β²) (y² + z²))½)
Теперь давайте совершим обратный переход в СО покоящейся среды. Заменим
u = x – vt
где vt – это положение источника в момент t.
φ(x, y, z, t) = q / (4πε₀ ((x – vt)² + (1 – β²) (y² + z²))½) ≡
≡ q / (4πε₀ (1 – β²)½ ((x – vt)² / (1 – β²) + y² + z²)½)
Это уравнение полностью совпадает с уравнением Фейнмана (21.39). Здесь Фейнман написал:

Однако, как мы видели, это не так: для вывода этих уравнений, мы из СО покоящейся среды перешли в СО источника, причем именно при помощи преобразования Галилея u = x – vt, затем обратно. И в обеих этих системах отсчета, уравнения для φ выглядят совершенно одинаково (единственная разница – замена u на x – vt). Потенциал φ в СО источника выглядит как
φ(u, y, z) = q / (4πε₀ (u² + (1 – β²) (y² + z²))½)
а вовсе не как
φ(u, y, z) = q / (4πε₀ (u² + y² + z²)½)
Это я и имел в виду, когда писал, что Фейнман дает формуле (21.39) совершенно неправильную интерпретацию, в частности, потому, что у него отсутствует переход из одной системы отсчета в другую при выводе этих уравнений.
Отредактировано: Yuri Rus - 25 фев 2020 17:59:59
ОТВЕТЫ (0)
Комментарии не найдены!